Implementation of Global Minimum Search using Particle Swarm Optimisation in CUDA
2021-06-11
MMI713 Applied Parallel Programming on GPU
Particle swarm optimization (PSO) is a population-based stochastic optimization algorithm motivated by intelligent collective behaviour of some animals such as flocks of birds or schools of fish - proposed by Eberhart and Kennedy. [4] The idea of PSO algorithm is inspired by two main research areas: evolutionary algorithms that makes it search a large region, and artificial systems projecting life attributes.
PSO can have results faster compared to other methods. Also, PSO does not require the function to be optimized to be differentiable, for it simply does not use the gradient of the problem unlike gradient descent. Also, the algorithm has a few hyperparameters that are easy to understand. Lastly, it is parallelizable due to the swarm nature of the algorithm itself. [4]
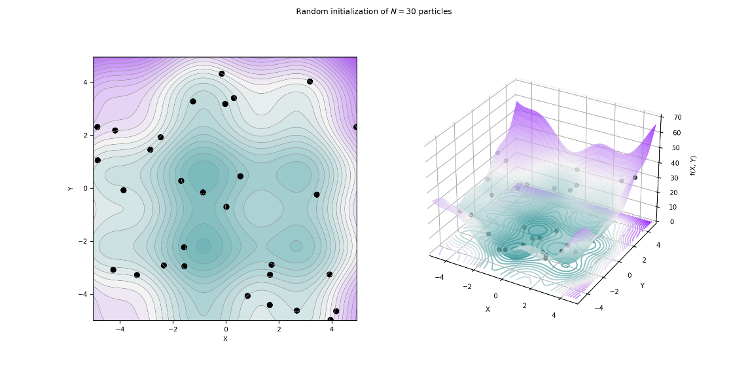
The main goal is to search for the global minimum of a function. This is firstly done by placing a particle swarm, randomly if chosen to be. This can be visualized as in Figure 1. Also, the velocities to update their position must be initialized. Then, the particles are made move according to a cost function employing a few simple formulae, also guided by their own best-known position in the solution space as well as the entire swarm’s best location. [3]
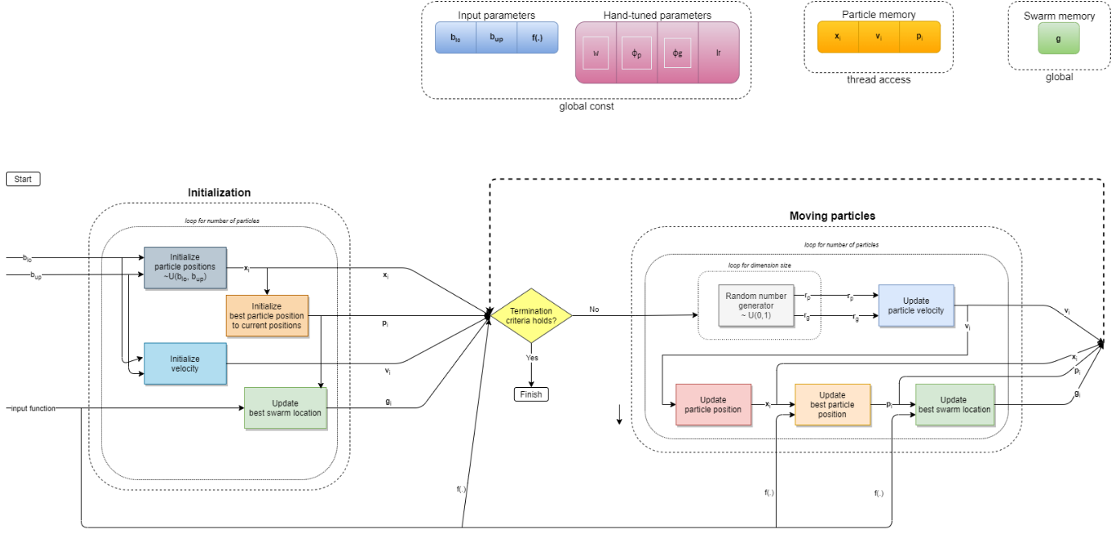
for each particle i = 1, ..., S do
Initialize the particle's position with a uniformly distributed random vector: xi ~ U(blo, bup)
Initialize the particle's best known position to its initial position: pi ← xi
if f(pi) < f(g) then
update the swarm's best known position: g ← pi
Initialize the particle's velocity: vi ~ U(-|bup-blo|, |bup-blo|)
while a termination criterion is not met do:
for each particle i = 1, ..., S do
for each dimension d = 1, ..., n do
Pick random numbers: rp, rg ~ U(0,1)
Update the particle's velocity: vi,d ← ω vi,d + φp rp (pi,d-xi,d) + φg rg (gd-xi,d)
Update the particle's position: xi ← xi + lr vi
if f(xi) < f(pi) then
Update the particle's best known position: pi ← xi
if f(pi) < f(g) then
Update the swarm's best known position: g ← pi
PSO has been proposed by Kennedy and Eberhart in 1995. [6] PSO has been applied in various areas, such as foreign exchange rate forecasting [1] and traffic accident forecasting [2]. It has been implemented in Python [5], Java, Matlab [6] and OpenCL [7], also in hardwares like FPGA.
The solution will require synchronization, using a sharing memory, and pointers reading the solution space in a parallel fashion that should be efficient considering race conditions or bank conflicts on memory access.
The solution to this problem is easily parallelizable for that only simple operations need to be executed for each particle or each dimension for all situations. There is a need for use of a shared memory between threads corresponding for a particle and a dimension.
Global minimum search, i.e., global optimization, problem is a branch of mathematics that attempts to find the global minima or maxima of a function on a given set. It is mostly called minimization problem since maximization of a real-valued function is the same as minimization of negative of the same function. Applications include many important problems: protein structure prediction, traveling salesmen problem, curve fitting, et cetera [1].
Particle swarm optimization (PSO) is a population-based stochastic optimization algorithm motivated by the intelligent collective behaviour of some animals such as flocks of birds or schools of fish - proposed by Eberhart and Kennedy. [2]
PSO can be purposed to solve the global optimization problem. However, when using large number of particles, complex functions or searching larger spaces, sequential nature of CPU can be crippling in terms of performance.
Due to its particle nature, PSO is suitable for parallelization. We have implemented parallel PSO algorithm on GPU using CUDA. Experiments are done in a laptop featuring Intel Core i7-6700HQ @ 2.60 GHz, 16 GB of RAM, CUDA version 11.2 and NVIDIA GeForce GTX 960M 8 GB having CUDA compute capability 5.0.
In this work, we implemented the Standard Particle Swarm optimization algorithm released in 2011 [4]. Differently from the basic PSO algorithm, it uses Adaptive Random Topology (ART) for its neighbourhood structure, choosing K neighbours that each particle is responsible to inform, which is a more suitable version for a GPU implementation. The neighbourhood relations are generated randomly in initialization and updated when global fitness does not improve. Also, velocity is updated in a geometrical way.
In the parallel implementation, each particle corresponds to a thread in the kernel. In other words, parallelization in this corresponds to the for loop on each particle in the swarm. The parallel algorithm starts with initializing all particles’ positions and velocities in a random fashion, and calculating the objective values corresponding to the position of each particle. Then, a neighbourhood matrix is generated randomly, in which for each particle K neighbours are chosen. Then, neighbour best values are updated using this matrix. The best fitness within the swarm is updated then, using atomicMin function of CUDA, that is based on atomicCAS accordingly with the NVIDIA implementation suggestion for devices with compute capability < 5.0. After updating position and velocity using particle positions, velocities, particle’s and neighbours’ best positions, the iterations continue with the pattern explained before, with the extension of creating new neighbourhood relations if no improvement is observed in the best fitness value.
We have defined nine (9) different device helper functions and a single kernel for this task, overall. These are as follows:
-
Random state initializer
-
Objective function evaluator
-
atomicMin
-
Different vectors checker
-
Random neighbourhood matrix generator
-
Random position initializer (spherical)
-
Position updater
-
Velocity updater
-
Neighbour best fitness updater
Shared memory is employed in the kernel for the best fitness, the particle positions, the particle fitness values and the neighbourhood matrix.
The algorithm is written also for the case of multiple runs, which is passed as a grid dimension parameter in the kernel. Multiple runs can be beneficial for real-world applications since PSO does not guarantee the global minima. Using more particles may not improve results after a point, and multiple random initializations will give better results or at least the same.
| # of runs | Objective function | CPU best fitness | CPU runtime (ms) | GPU best fitness | GPU runtime (ms) |
| 1 | Sphere | 3.21 | 224 | 0.90 | 235 |
| 1 | SchafferF7 | 2.87 | 264 | 2.80 | 234 |
| 50 | Sphere | 0.53 | 12690 | 0.45 | 518 |
| 50 | SchafferF7 | 0.32 | 12246 | 0.52 | 523 |
| # of particles | Objective function | CPU best fitness | CPU runtime (ms) | GPU best fitness | GPU runtime (ms) |
| 32 | Sphere | 3.21 | 224 | 0.90 | 235 |
| 32 | SchafferF7 | 2.87 | 264 | 2.80 | 234 |
| 64 | Sphere | 0.92 | 440 | 0.27 | 255 |
| 64 | SchafferF7 | 1.55 | 583 | 2.04 | 255 |
| # of dimensions | Objective function | CPU best fitness | CPU runtime (ms) | GPU best fitness | GPU runtime (ms) |
| 10 | Sphere | 3.21 | 224 | 0.90 | 235 |
| 10 | SchafferF7 | 2.87 | 264 | 2.80 | 234 |
| 20 | Sphere | 8.08 | 522 | 7.76 | 451 |
| 20 | SchafferF7 | 9.76 | 583 | 7.32 | 455 |
| 50 | Sphere | 16.49 | 1322 | 16.57 | 1221 |
| 50 | SchafferF7 | 16.37 | 1339 | 12.62 | 1218 |